P=0 p = 0 とすれば5を得る。 ( a 0 = 1 a^0=1 a0 = 1 であることから直接分かる,この方が素直) なお,6については 底の変換公式の証明と例題 で詳しく解説しています。 1~6を使えばほとんどの対数の計算問題を突破できますが, 覚えておくと便利な対数の対数の計算法則の使い所 対数は多くの学生が苦手とするところですが、その大きな要因の1つがこれら 計算公式の乱用 です。 定義も考えず、ただ公式に当てはめるだけのパズルゲームにした途端、対数はその魅力を全て失います。 例えば、対象高2 再生時間1458 説明文・要約 ※ log a b について、b のことを「真数」という (1)真数部分の掛け算は、対数としては足し算に分解できる (例)log 2 28=log 2 4+log 2 7 (2)真数部分の割り算は、対数としては引き算に分解できる
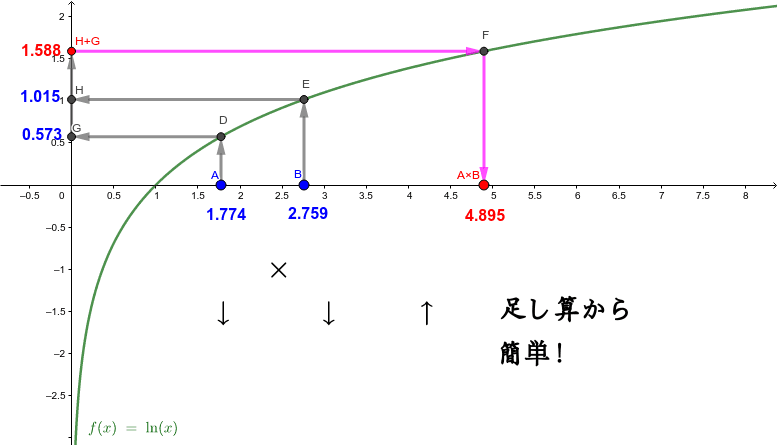
対数関数y ln x の性質 Geogebra
対数 掛け算 足し算
対数 掛け算 足し算- そして、logの足し算は掛け算じゃないかっていう話は確かに対数法則にはありますけどこの計算には別に関係ないと思います! log26log25=log26×5 みたいなんとごっちゃになってますよね多分🤔 落ち着いて普通の分数計算だと思ってやってください。対数を取って計算することにより,掛け算が足し算になる。 195×417≒813 ( 実 際 の 計 算 は195×417=) 例題2 7÷173 を 計 算 せ よ 。 ( 解 答 )常 用 対 数 表 よ り log 7≒ ,log 173≒




対数で掛け算を足し算に変換 対数の2つのメリットを解説
これは今証明した1つ目の性質を使えば証明できます。対数の足し算は真数の掛け算でしたので、それを逆に使いましょう。 どういうことかというと $$\log_{a} b^{c}$$ という式はこう考えることもできます。 $$\log_{a} b^{c}=\log_{a} (b\times b\times \cdots \times b)$$Iii) 対数の計算 対数は,整数部(指標)と小数部(仮数)からなるが,小数点以下の数字が有効数字となる. 間違いやすいので注意すること. 例)24 x 103,24 x 104,24 x 105の常用対数を計算せよ. log(24 x 103) = log 24 log103 = log 24 3 = 掛け算の裏技 足し算や引き算の速算は、元々計算力が高い人にとってはそこまでの有り難みはない。 しかし、掛け算の速算は通常の数倍の速度で計算が可能になる。 掛け算こそ速算術が最も威力を発揮する 演算である。
4.対数関数の微分 対数関数を微分する(詳細略)と,以下のようになる。 (log a x)' = 1 / (x × log e a) ここで e は (1 t) 1 / t → e (t → 0) となる定数である。 そこで,逆に「導関数が 1 / x となるような対数」を考え,これを自然対数と言う。対数とは、数学の概念の一つである。 指数の反対の概念。 概要 手計算を行う際、足し算や引き算に比べて掛け算や割り算は時間がかかる。 累乗はさらに時間を要する。計算機がまだ開発されていなかった頃、数値の計算には多大な時間を要した。対数を使うと掛け算は足し算に、 割り算は引き算に、 指数関数は掛け算に変換できるという原理を利用しています。 たとえばlog2≒03、log5≒07であることを利用して2×5を求めると、 log(2×5) = log2 log5 = 0307 = 1 =log10
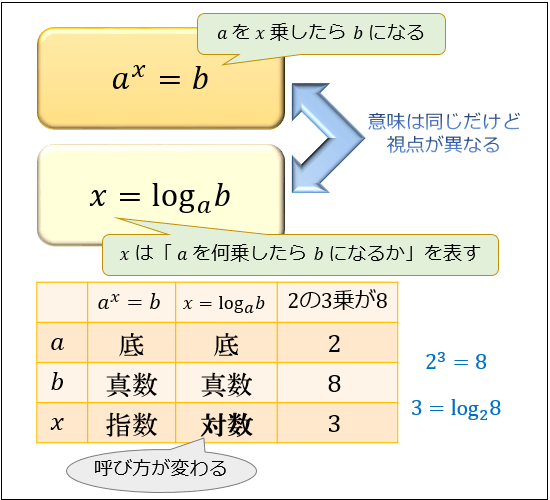
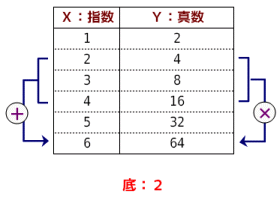
本稿では、 対数を用いると計算がラクになる ということを見ていきます。 つまり、 掛け算は足し算になる 割り算は引き算になる 指数は定数倍になる ということを見ていきます。 対数の基本 まず、対数の基本をおさらいしておきましょう。高校生 2年以上前 国強になりたい (4) (5)がわかりません log同士の掛け算ってどうやればいいのでしょうか (3)は底を変換すれば解けましたが、この2問は解ける気がしません 地球と太陽の距離 ューンジ 各/SIGのゆめ2思 太陽からの 1 ) い こし 2 う 次対数表はJ Napier ()が作り上げた数表で、掛け算を足し算に変えてしまうための表です。 a x ×a y =a xy ですが、a x =p, a y =q である時、逆にpにxを対応させる関数log a をp ↦x (xは a x =pとなるx)と考えます。




対数の計算法則 なぜ掛け算が足し算に 対数の計算は定義を見返そう 青春マスマティック



対数の計算
であり、現代的な対数と違って、かけ算を足し算に、割り算を引き算に変える目的だけで作られている(乗算と除算を容易にしたいだけなので、底は固定値で良い)。 この p のことを ネイピアの対数 (Napierian logarithm)という。 ネイピアは 1594年 にこの対数の概念に到達し、この定義を用い 年間計算を続け 7桁の数の 対数表 を作成し 1614年 に発表した。 指数対数の問題で掛け算は足し算に、割り算は引き算にしますよね?逆に足し算は掛け算に、引き算は割り算にしますか?するのでしたら、なぜそのような事になるのか教えてください。 数学 締切済 教えて!goo対数を使うと掛け算は足し算に、 割り算は引き算に、 指数関数は掛け算に変換できるという原理を利用しています。 たとえばlog2≒03、log5≒07であることを利用して2×5を求めると、 log(2×5) = log2 log5 = 0307 = 1 =log10 ⇒ log(2×5) = log10 ⇒ 2×5 = 10 といふうに




Log同士の足し算ってかけ算になって Log同士の引き算って割り算になりますか Clear



緊急です 数iiの問題で Logの足し算は掛け算にすると教わ Yahoo 知恵袋
定義 対数は次のように定義され、記号 log を用いて表されます。 M = ap (a ≠ 1, a > 0, M > 0) M = a p ( a ≠ 1, a > 0, M > 0) という関係があるとき、 p p を a a を底(てい)とする M M の対数といい、 p = loga M p = log a M と表す。 M M を 対数 p p の真数という。 この対数(logarithm)の発明と対数表の作成 安全な航海のため 天文学の計算(文字通り天文学的数の掛け算)を スコットランド 数学者、物理学者、天文学者、占星術師。 対数の発明者、対数表の作成。 かけ算を足し算に、割り算を引き算に。 対数の計算って 足し算→掛け算 引き算→割り算 掛け算→足し算 割り算→引き算 ですか?




ゼロが多い数でも簡単 計算をラクにする方法 中高数学おさらい 指数 対数 文系でも怖くない 学び直し 数学 ダイヤモンド オンライン




対数 とは わかりやすくまとめてみた 初心者向け もんプロ 問題発見と解決のためのプログラミング
対数不等式 常用対数 センター問題0609 → スg スム版は別包ソス ス ス ス@ スi スe スw ス スヤ) スホ撰ソス スv スZ ス@ ス ス ス@ ス ス スフペ ス スW スヘ, スホ撰ソス スv スZ ス ス スg スノ付 ス ス スネゑソス ス ス ス ス スl ス ス ス ス スノ, ス「対数」と聞くだけで拒否反応が出るかもしれません。 私も 年前のことですから「対数」についてはすっかり忘れました。 しかしながら、「計算尺が対数を利用したもの」で、「対数での足し算は、かけ算」、「対数での引き算は割り算」になると言われ とすると、対数を使って u v = log x ・・・(3) だから、(1)、(2)と(3)から結局 log x = u v = log y log z つまり、 となる。対数を考えれば、掛け算は足し算になる。 ということで、a を b 回掛けた数を c とすると、



対数について 計測制御 Labview徒然草 By 成田義也




指数対数関数 怜悧玲瓏 高校数学を天空から俯瞰する
すべての対数の底を2または5に統一する \\2zh 左の括弧内は2,\ 右の括弧内は5で統一したくなるが,\ 全て同じ底に変換するのが結局は近道である \\1zh 右の括弧内は対数が分母にある和なので,\ \log_aM\log_aN=\log_aMN による合体はできない \\2zh そこで,\ \bm②相対誤差は、100 から 999 までその対数に従って変化する。 ③典型的な数値として 500 をとると、log 10 a = log 10 5 05、として a(= 158)で有効数字の桁を変化させれば、有効数字の掛け算(割り算)の誤差の不連続性を小さくできる。第一法則 「掛け算は足し算に」 このように掛け算は指数において足し算になります。 第二法則 「割り算は引き算に」 分子にある が分母にある の数だけ割られて1になりますから割り算は指数の引き算になりますね。 第三法則 「累乗は掛け算に」




ニュートン式 超図解 最強に面白い 対数 ニュートンプレス



高校数学 B指数対数についてです 受験生です すごく根本的な Yahoo 知恵袋
四則演算がイラスト付きでわかる! 足し算・引き算・掛け算・割り算の総称。 概要 四則、加減乗除とも。 各々、以下の 掛け算は足し算に比べて計算が面倒だ。 やる夫 小数点の計算とかあんまりやりたくないお。 やらない夫 そこで一般的には尤度関数の対数をとったもの、対数尤度関数を使う。 対数 「掛け算を何回繰り返してその数字が作られたのかを調べる」計算 の対数は log (ログ 10 万) と表記する log の計算結果は 5 対数は英語で logarithm (ロガリスム) なので log のように表記されます。 対数はあくまで「 累乗の




対数関数y ln x の性質 Geogebra



対数で掛け算を足し算に変換 対数の2つのメリットを解説
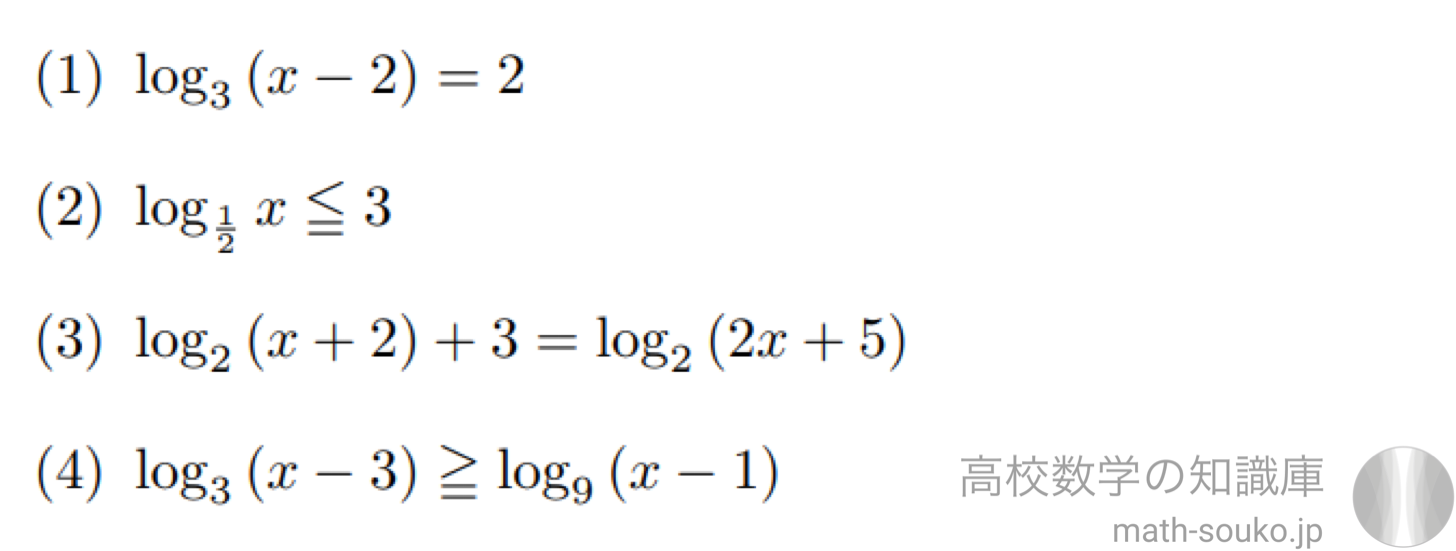



対数方程式と対数不等式の解き方 高校数学の知識庫




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook




と の疑問です は対数の性質で足し算を掛け算にまとめていますが 数学 教えて Goo
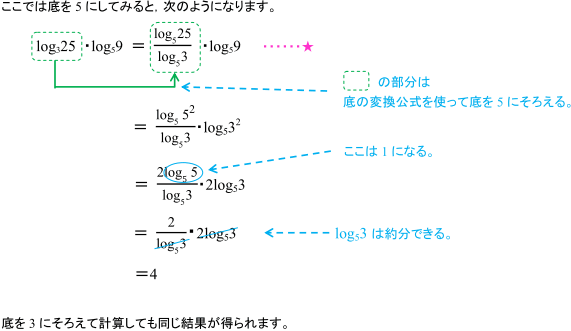



底をそろえて計算するときの底の決め方 数学 苦手解決q A 進研ゼミ高校講座
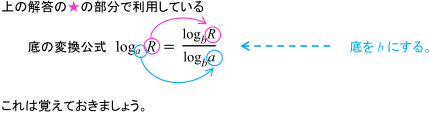



底をそろえて計算するときの底の決め方 数学 苦手解決q A 進研ゼミ高校講座




対数関数とは Logの基礎から公式やグラフまで解説 高校生向け受験応援メディア 受験のミカタ



対数の計算は足し算は真数の掛け算になって引き算は真数の割り算になると思うんで Yahoo 知恵袋



掛け算 を 足し算 で 計算 計算尺 Bar Soryu Shi
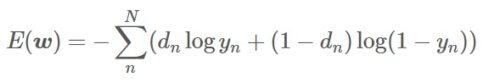



対数で掛け算を足し算に変換 対数の2つのメリットを解説




対数の足し算は真数の掛け算 ゼロからわかる対数その2 Youtube




と の疑問です は対数の性質で足し算を掛け算にまとめていますが 数学 教えて Goo



Logの計算するとき Logの足し算は掛け算になりますが Lo Yahoo 知恵袋



Q Tbn And9gcsmzu4yxdpscnm9nk3sp3ko0 Ag8sahcn Bnp1x19yodulopepg Usqp Cau




高2 数学 桁数の問題 北里大学18 高校生 数学のノート Clear




E E Iœvzz ª U E Ae A E Amazon De Bucher




対数とは Logって何 対数関数について基礎から解説 高校生向け受験応援メディア 受験のミカタ




対数とは Logって何 対数関数について基礎から解説 高校生向け受験応援メディア 受験のミカタ



1
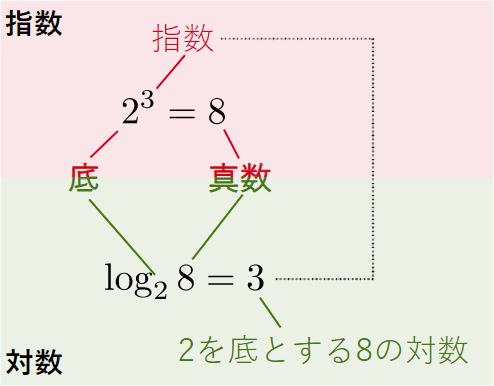



Ai 機械学習の数学 番外編3 指数と対数 対数編 Ai 機械学習の数学入門 It




対数 Wikipedia




計算尺 In 科学技術の礎 いしずえ




対数 Log の計算と公式 これでもうバッチリ Kenブログ 風のように しなやかに




対数関数 Log で1カ月悩んだ高校生が15分の解説でスッキリした話し マナビバ ー 個別指導ヒーローズから始める学びのポータルサイト



Logどうしの掛け算の方法を教えてください 一般的に言えば Lo Yahoo 知恵袋



指数と対数 その2 累乗と累乗根 対数グラフ ふシゼン




丸がついている部分 なぜlogが同じだったらかけ算に 直すのに直さず 高校 教えて Goo
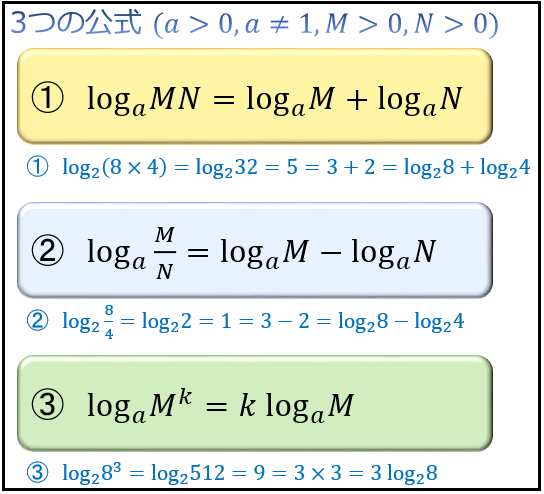



対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ



対数の計算




この 1 の計算 普通に掛け算して消していってるのですが なんかlogの掛け算は足し Clear
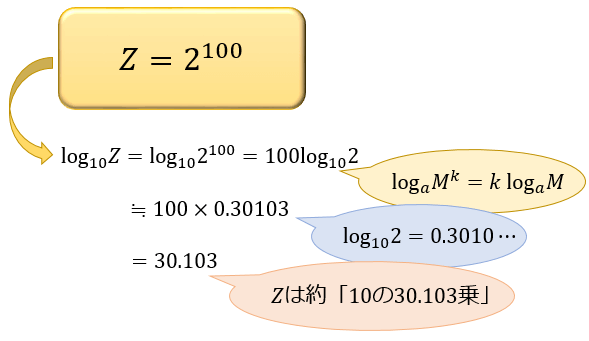



対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ




学校だと対数は 指数の逆関数 として習うだろうが 歴史的には指数よりも対数の方が早く考案されており しかもその動機が 大きな数同士の掛け算が対数を使えば 足し算になって 素早く計算できるため だという話はなかなか意外なので毎回演習テキストの脚注に載せている




Logの足し算は掛け算で計算するのじゃないんですか なぜここは通分なんですか Clear



Www Junten Ed Jp Contents Wp Content Uploads 13 04 9b5c677aee1fcff2c32f98 Pdf



常用対数



重い電車を動かそう リニアモーターの原理 工学のトビラ 九州工学教育協会 九工教




Newtonライト2 0 対数 ニュートンプレス




対数関数とは Logの基礎から公式やグラフまで解説 高校生向け受験応援メディア 受験のミカタ




掛け算を足し算で考える ログ Log キソカラ




対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ
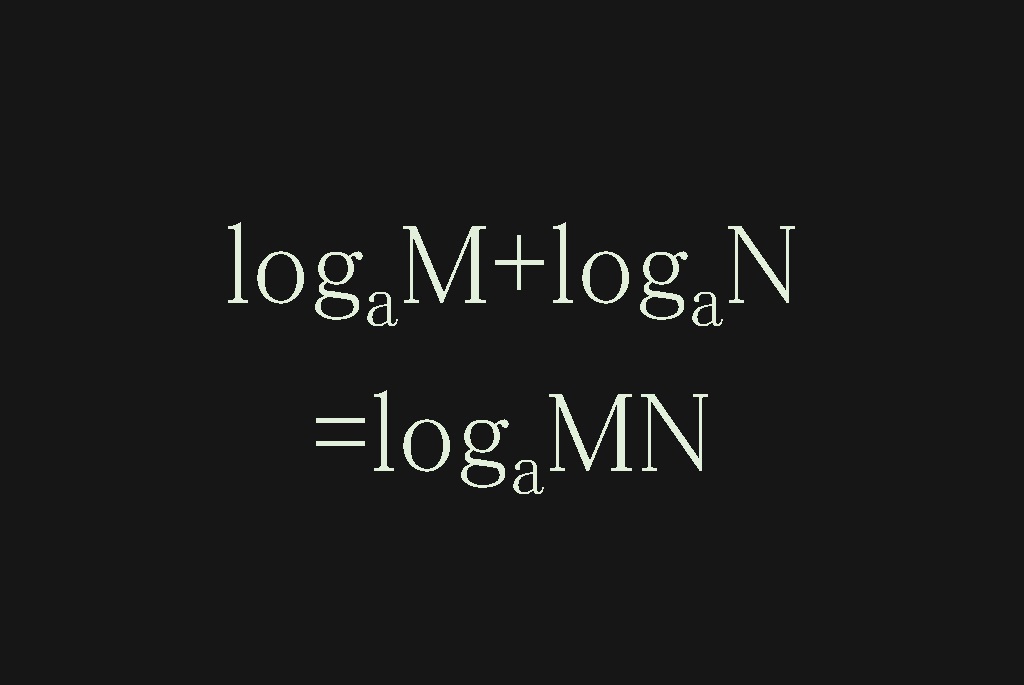



対数の性質と計算ルール 統計学が わかった




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook



対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ




小 中 高の計算がまるごとできる 足し算 引き算から微分 積分までの通販 間地 秀三 紙の本 Honto本の通販ストア




ট ইট র Norihito4 昨日録画した Bsキャンパスon 数学の歴史 第10回 対数から積分法へ を視聴 待ってました 計算尺 の登場 ヘンミno 2664sを使用し 掛け算を対数目盛による距離の足し算で表していることを解説 2 3 6 を Log 2 Log 3 Log



48s96ub7b0z5f Net Shisuu Keisan



底の変換公式



対数関数のこの式 なぜすべて なのに掛け算をすることが出来る Yahoo 知恵袋
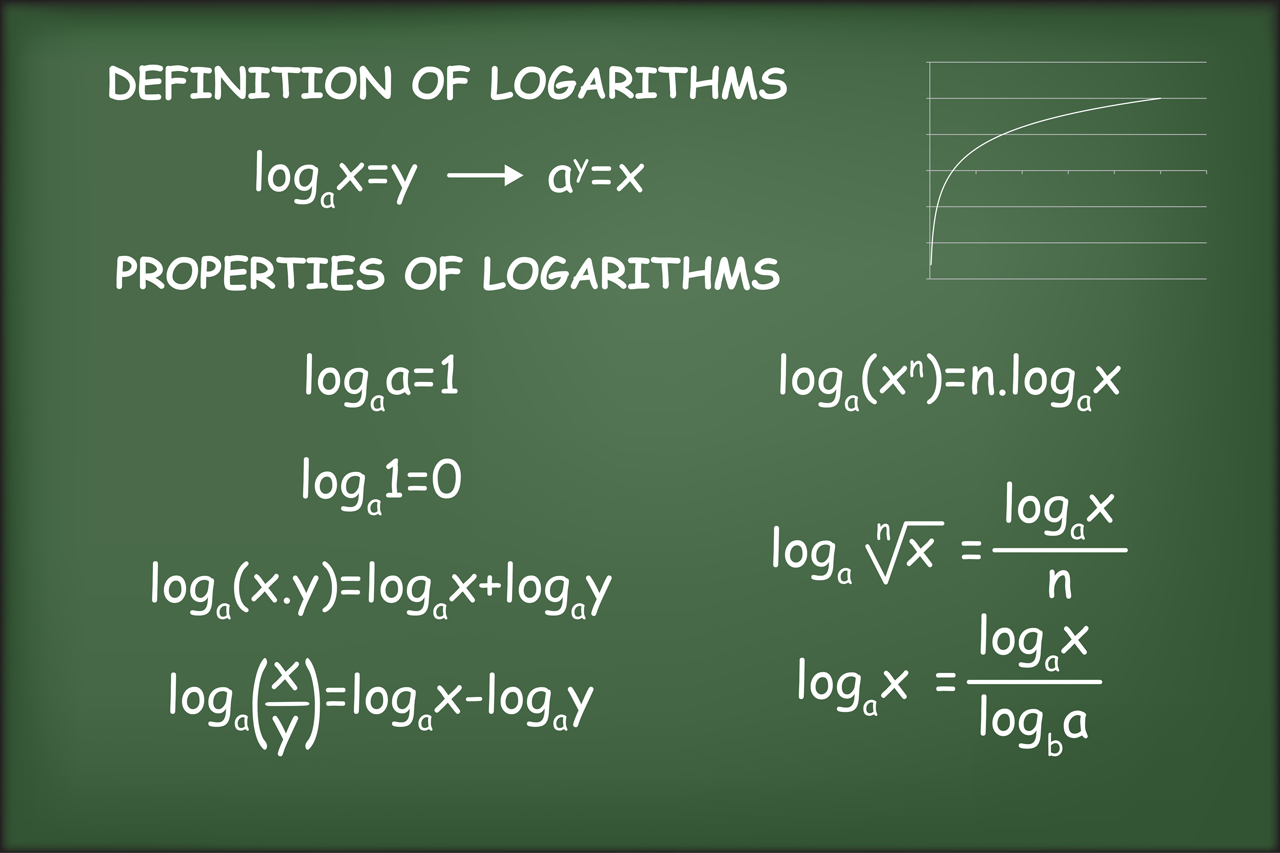



Ai 機械学習の数学 番外編3 指数と対数 対数編 Ai 機械学習の数学入門 It
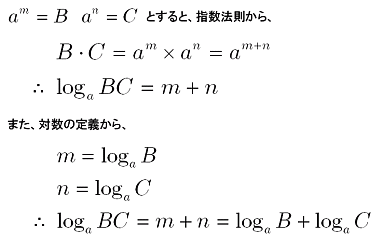



対数 対数の計算公式 大人が学び直す数学




対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook




O Xrhsths ラクシア Esシミュの人 Sto Twitter すごいざっくりと説明すると対数使えばこんな感じで 倍率を足し算で計算することができるというお話 こいしちゃんさんが言っているように枠被った瞬間に崩壊しますがそれはいつもの掛け算も似たようなものなのでね



数学iiです対数関数 1 です なぜこのlogの足し算は普通に足 Yahoo 知恵袋




数学 基礎講座 ネイピアと対数 Youtube



対数表




掛け算を足し算で考える ログ Log キソカラ




文系のためのめっちゃやさしい 対数 ニュートンプレス



数列 自然対数の意味 大人が学び直す数学



底も真数も同じ対数の掛け算ってどうやって計算しますか 図のような計算って Yahoo 知恵袋
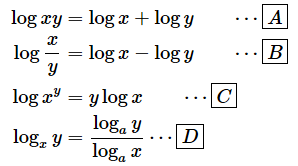



Ai 機械学習の数学 番外編3 指数と対数 対数編 Ai 機械学習の数学入門 It




数学 対数関数 対数の計算 オンライン無料塾 ターンナップ




対数で掛け算を足し算に変換 対数の2つのメリットを解説



対数とは 対数のメリット 指数との関係 制御工学の基礎あれこれ



対数




対数で掛け算を足し算に変換 対数の2つのメリットを解説



1




Aeton この2日間で取り組んだ数学研究 初等巨大数研究の一環で ただの足し算をあえて掛け算 累乗 対数で近似表現する試み おこじょ数の基礎を成す演算でもある 色々やってみた結果 Eの凄さを目の当たりにすることに



数学用語解説 数 指数関数と対数関数
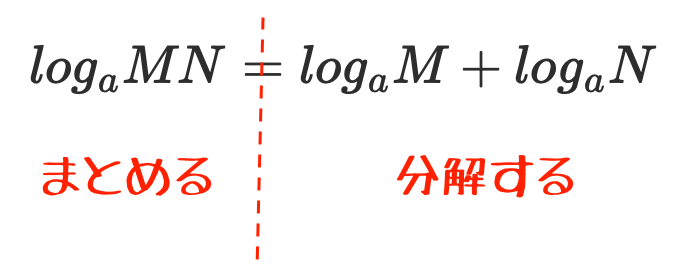



対数の計算法則 なぜ掛け算が足し算に 対数の計算は定義を見返そう 青春マスマティック



Logの足し算 引き算についてです Logの底と真数が同じ Yahoo 知恵袋




対数とは何なのかとその公式 メリットについて 対数をとるとはどういう意味か アタリマエ




赤いマーカー部分のlogの計算は足し算なので掛け算するのでは無いのですか Clear




対数関数 Logの意味と頻出公式まとめ 底の変換公式と裏ワザも紹介 ますますmathが好きになる 魔法の数学ノート



対数は 震度にも 音楽にも 理科のphにも使われている




なぜ上はlog同士を足し算 引き算しているのに対し Clear




ট ইট র Norihito4 昨日録画した Bsキャンパスon 数学の歴史 第10回 対数から積分法へ を視聴 待ってました 計算尺 の登場 ヘンミno 2664sを使用し 掛け算を対数目盛による距離の足し算で表していることを解説 2 3 6 を Log 2 Log 3 Log




オナラの成分半分で ニオイ も半減するか くさいは 足し算 ではなく かけ算 2ページ目 President Online プレジデントオンライン




Aeton この2日間で取り組んだ数学研究 初等巨大数研究の一環で ただの足し算をあえて掛け算 累乗 対数で近似表現する試み おこじょ数の基礎を成す演算でもある 色々やってみた結果 Eの凄さを目の当たりにすることに



対数法則で真数掛け算を対数足し算で表す方法論について もやもやし Yahoo 知恵袋



Q Tbn And9gcssccaemn1yacv7ojwjbfsp0d4d31mdmtpm0k5x6wtctg6mkcxo Usqp Cau




指数関数 対数関数講座その1 計算練習 高校数学の知識庫




指数法則を使う問題の計算練習 高校数学の知識庫




一刀両断 Logが Phへと導かれる仕組み 夢のバケ学



統計学的画像再構成法である




下線部のところなんですけどlogって足し算はかけるんじゃないんですか Clear



底の変換公式




掛け算を足し算で考える ログ Log キソカラ




対数の加法と減法 対数関数 数学の部屋




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook
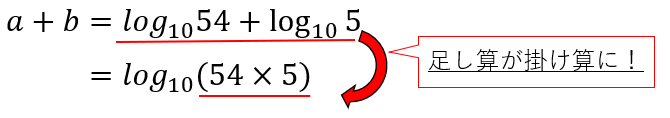



掛け算を足し算で考える ログ Log キソカラ




指数 対数関数の公式 指数法則と対数法則と底の変換公式の証明 Irohabook
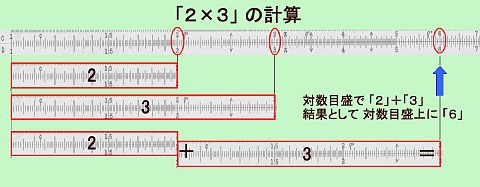



計算尺 2in 科学技術の礎 いしずえ


