分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題 中1方程式 分数が含まれるときの解き方を問題解説 Youtube 中1 1次方程式 でつまずく原因と解決法 分数 分数の入った方程式 Youtube 3分でわかる 分数をふくむ連立方程式 次の 2 つの連立方程式 と、 を、 解く前の子に、 「どうする?」と聞きます。 すぐに、 2 番目の式を、 1 番目に代入する・・ようなことを答えてくれます。 この子に、 さらに聞きます。 「何を、どこに?」です。 少し考えてから、 でしたら、 「 y を、1 番目の x に」のように 答えてく連立方程式の中に分数の項が混じってる場合の解き方。 漫画で紹介したように、連立方程式の中に分数の項が混じっている問題はどう解いたらよいでしょうか? 簡単です。 一次方程式のときと同じく、 「分母、邪魔!」 と考えて、分母が消えるような数を

いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者
分数の連立方程式 解き方
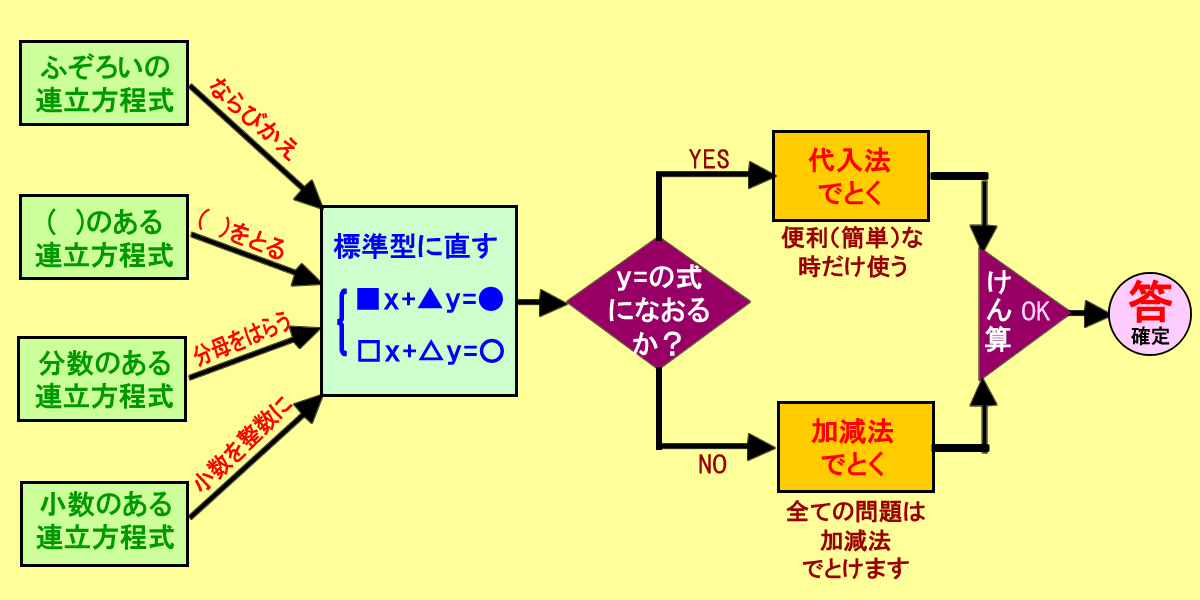
分数の連立方程式 解き方- 分数を含む二次方程式 というモンスターが出現することがあるんだ。 今日はこのパターンの二次方程式の解き方をマスターしていこう。 3分でわかる!分数を含む二次方程式の解き方 たとえば次のような問題があるよ。1つの方程式の両辺を何倍かしただけでは係数がそろわないときは、それぞれ何倍かしてそろうようにします。 これは分数の通分と同じ考え方です。 この問題では (1)を4倍する と −12y ができ、 (2)を3倍する と 12y ができるので、足し算により y が消去でき



Iseqi Pukiwiki
移項とは?1分でわかる意味、やり方、符号、ルール、分数との関係 1次方程式の解き方と計算問題 1次方程式を解き方はシンプルです。 ・左辺に未知数x、右辺に数となるよう移項 ・「x=」の形になるよう、係数や項を整理 これだけです。連立線形微分方程式 {x ′ = ax by y ′ = cx dy について いずれか一方の関数の線形2階斉次微分方程式に帰着させて解くことができるようになります。 微分演算子を用いた表現により,連立方程式を解くことができるようになります。 係数行列の対角化に ・ 連立方程式を進んで解こうとする。 ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。 ・ 加減法による連立方程式の解き方(2つの式をたしたりひいたりして解く)を理解する。
連立方程式の解き方がわかる方教えてください。 日商簿記一級、部門別原価計算の相互配賦法、連立方程式法です。 a=6/26b4,500,000 b=3/18a4,250,000 答え a=5,700,000 b=5,0,000 になるのですが、解き方がわからずに困っています。 ①分数をふくむ方程式の解き方(1) まず、下の方程式を見て下さい。 文字の項も数の項も、すべての項に分数がふくまれています。 分数をふくむ方程式をそのまま計算するのは、大変そうですよね。 じつは小数の方程式と同じように、分数をふくむ方程式も、 すべて整数の方程式 にする連立方程式を解くには,xかyのどちらかの文字を1つ消去して,文字が1つだけの方程式にして解く。 この解き方に 加減法 と 代入法 がある。
続いては小数を含む方程式の解き方です。 係数が小数の場合は、両辺を $\textcolor{blue}{10}$ 倍 ($\textcolor{blue}{100}$ 倍 )して式を簡単にします。 問題次の連立方程式を解きなさい。復習連立方程式の解き方 連立方程式とは、一般的に \begin{eqnarray}\left\{\begin{array}{l}axby=c\\dxey=f\end{array}\right\end{eqnarray} といった形で表すことが多い式です。 2元1次方程式と呼ばれる「2つの変数(文字)」と「最大次数が1」の式で表されます。 連立方程式二 5 2 連立方程式の解き方を調べる。 ・加減法 ・代入法 ・有効な解法 ・かっこ,小数,分数 を含む連立方程式 ・a=b=c の形の連立 方程式 一元一次方程式に帰着して解を求 めさせるために,文字を1つ消去す る方法を説明させる。



分数のある連立方程式の代入法の解き方



連立方程式 代入法2 チーム エン
基本編 (分母に文字がある連立方程式) 分母に文字がある連立方程式の解き方です。 次の連立方程式を解きなさい。 - - - { - 2 x - 8 y = 6 1 x 2 y = - 5 ※答えは こちら で確認してください。 こういった分母に文字がある連立方程式を解く場合は 1 x = A 例題 かっこ,分数,小数を含む連立方程式1 次の連立方程式を解きなさい。(1) \(\begin{cases}2x\left( 3y\right) =4&\cdots ①\\ 3\leftかっこをふくむ連立方程式や、分数・小数をふくむ連立方程式、文字が3つの方程式など、いろいろな連立方程式の解き方を練習する問題プリントです。 いろいろな連立方程式 練習問題 (1) 答え いろいろな連立方程式 練習問題 (2) 答え いろいろな




中学数学2年 連立方程式の解と係数 受験の月




分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題
分母にxの解き方! 分数の方程式は、とにかく 分母をはらう! というのがポイントとなります。 それは分母に\(x\)があっねらい ・ 連立方程式を進んで解こうとする。 ・ 連立方程式を解くには、既習である文字1つの方程式を導けばよいことに気付くことがで きる。 ・ 加減法による連立方程式の解き方(2つの式をたしたりひいたりして解く)を理解する。 段階 学習活動連立方程式 要点 連立方程式の解き方(加減法,代入法) いろいろな連立方程式 連立方程式(小数・分数) 連立方程式の文章題1 連立文章題 速さ 連立文章題 割合



中2数学連立方程式文字が分母にある問題です 解き方を教えてく Yahoo 知恵袋




一次方程式の解の求め方 数学fun
しかし異なる方程式が2つあれば x と y の値を求めることができます。 そのため連立方程式という解き方があります。 連立方程式の解き方には、 加減法 と 代入法 の2つの計算方法があります。 分数がいるときは要注意! テストでも間違えやすいところなんはじめてこの問題を解いてみて、この解き方が思いつかないのは当たり前 でも、 どうしたらいつもの形になるかって視点を持つことは大事 だよ よし、これでいつもの連立方程式と同じだね ③より、 A = B − 5 2 A = B − 5 2 これを④に代入して、 8B− 2B 1次方程式の解き方はルールを覚えれば簡単 今回扱うのは「 1次方程式 」です。 みなさんは新しく「方程式」という内容を学習していきますが、この方程式は数学において非常に非常に役に立つものですから、ぜひ身につけていきましょうね!



連立方程式の利用の問題です この答えは分数で解いてある Yahoo 知恵袋




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット
「連立方程式の解き方って、 "加減法・代入法"の 両方ができないとダメですか? 」 大丈夫、安心してください。 結論から言えば、 「自分の解きやすい方法」でOKです。 どちらの解き方も 同じ答え になるので、 "正しい答え"に どちらでも到達でき 連立方程式は、未知数が2つというのがネックになっています。1つになれば、普通の方程式として解くことができる訳ですから、 何とかして未知数を1つにする ことが、連立方程式の解き方の基本となります。 それぞれ見ていくことにしましょう。 代入法分数の連立方程式 解き方は両辺に数をかけて分母を消すんだ 中学や高校の数学の計算問題 3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく 中1 1次方程式 でつまずく原因と解決法 分数




連立方程式の加減法の解き方をマスターしたい方は見てください 中学や高校の数学の計算問題



1
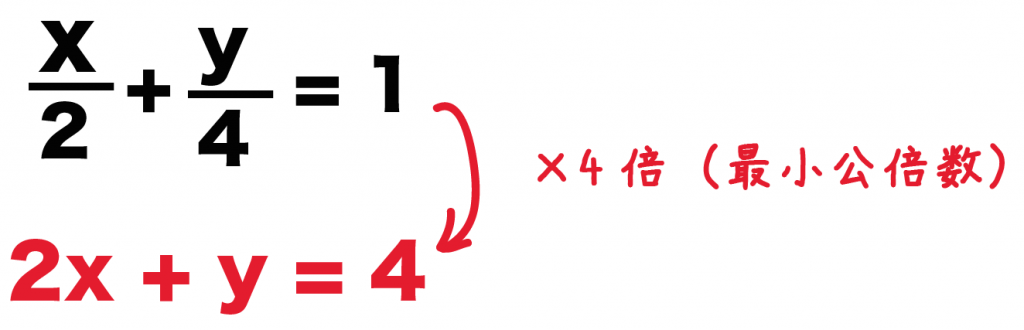
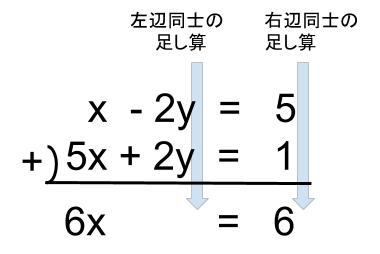
2つの未知数 x, y のどちらかの 係数が等しいとき は、左辺どうし、右辺どうしをそれぞれ 引く と1文字を消去できます。 この問題では y の係数がそろっているので、 y が消去できて x だけの方程式になります。 →(3) (3)の結果を(1)か(2)のどちらかに代入すると、もう一つの未知数も求まります。 分数入りの連立方程式の解き方がわかる3ステップ つぎの3ステップでとけちゃうよ! 例題をときながらみていこう! 例題 つぎの連立方程式を解きなさい。 $$\frac{x}{2} \frac{y}{4} = 1$$ $$3x 2y = 5$$ Step1 分数をけすっ! 分数を消しちゃおう! 方程式から分数連立方程式の解き方のまとめ 式がまとまっていないものはまとめる。 分数や小数の入った式は、整数の式に直す。 「連立方程式




中2数学 連立方程式 いろいろな連立方程式 4つのパターン たけのこ塾 勉強が苦手な中学生のやる気をのばす




3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく
プライバシーポリシー 免責事項 19–21 方程式の解き方まとめサイト 免責事項 19–21 方程式の解き方まとめサイト 10倍、100倍して小数を消せばいいよ! というわけで、今回の記事では「小数を含む連立方程式の解き方」についてイチから解説していきます。 今回の記事では以下の問題の解き方について解説していくぞ! 次の計算をしなさい。 ① ② ③ 方程式の基本方を復習しました。この節ではそれを前提に連立の2次方程式の解き方を紹介し ます。 連立2次方程式の一般論はかなりの準備が必要となるのでここでは扱わず,後 で必要となる特別な形の方程式の解き方だけを身につけてもらうことを目標とし ています。1




連立方程式の解き方 中学生 数学 公式 家庭教師のアルファ プロ講師による高品質指導
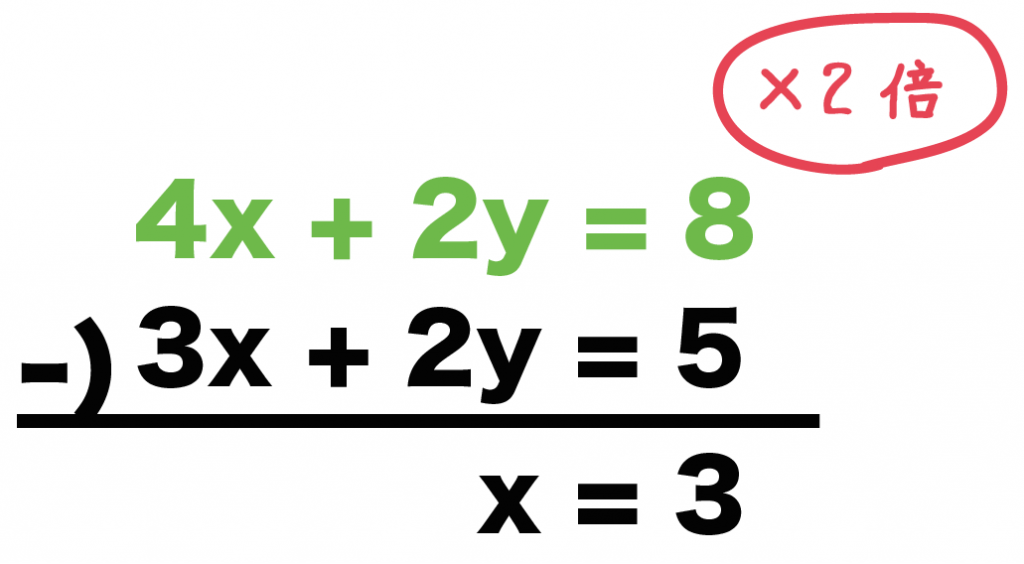



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく
株式会社スプリックスの授業動画 中2数学 連立方程式の解き方 その3(かっこ・小数・分数)ポイント・連立方程式を解く準備 ・かっこをふくむ == 連立1次方程式の解き方(まとめ) == 連立1次方程式とは,次の形の方程式をいい,一般に未知数をn個含む1次方程式から成り立っている.このページでは未知数が2個~4個の場合を扱う.二次方程式は「①解の公式②因数分解③√」による解き方で解きます。 こんにちは、ウチダです。 今日は、中学2年生で習う 「連立方程式」 について詳しく解説していきます。 「連立方程式とは何か」をまず知り、絶対に押さえておきたい方程式の性質を理解した上で、代入法と加減法の2つの計算方法での解き方をマスターしていきましょう^^ この記事を読



中学2年 数学 連立方程式 解き方 分数係数の方程式 計算練習問題



2 02 03 2a1 Gif




たけのこ塾 中2数学 今回は 連立方程式の計算問題 を作成しました カッコや分数を含むと連立方程式の解き方を しっかり復習しておきましょう 詳しくは画像の解説をご覧下さい 勉強垢 中2 数学 連立方程式 Youtube T Co Waess9diai




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




中学数学2年 いろいろな連立方程式 係数が小数 係数が分数 A B C型 受験の月




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト




教えて下さい 連立方程式が分数の場合はどうやって解けばいいんですか Clear




Akiya Su Auf Twitter 数学 連立方程式 濃度 昨日の答えと難題 分数や小数がある方程式の解き方も確認しておこう 中学数学 連立方程式 濃度




中1 数学 中1 30 方程式を解く 小数と分数編 Youtube



Iseqi Pukiwiki
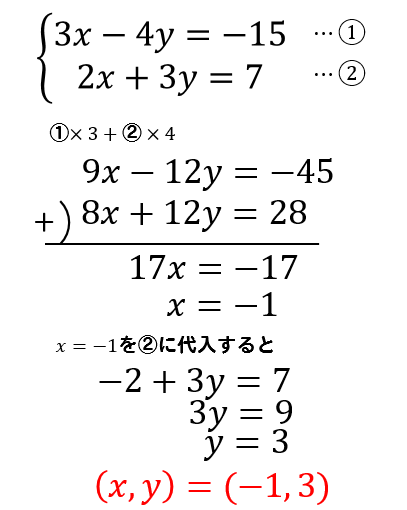



連立方程式 加減法の解き方をわかりやすく問題を使って徹底解説 数スタ




連立方程式 分母の数が大きい場合の計算 中学生からの勉強質問 数学 進研ゼミ中学講座




分数の連立方程式の解き方を教えてください で何を考えたら答えを導き出せるのか教えて Clear




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学



2 27第2章いろいろな連立方程式 分数を含む連立方程式 プログラミングの雫




方程式の解き方まとめ 中3生は必見 これで受験を乗り切ろう 中学数学 理科の学習まとめサイト




連立方程式 分数を含む計算の解き方をイチから解説 Youtube




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点




中学2年生 数学 いろいろな連立方程式 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




分数が含まれている連立方程式の解き方 全国 中学数学ができるようになるブログ



3




分数の連立方程式 Youtube




連立方程式を小学生に教える




中学数学 連立方程式 の効果的な教え方 小数 分数問題




分数が含まれている連立方程式の解き方 全国 中学数学ができるようになるブログ



連立方程式の問題です これは分数の計算です 解き方と式と答えを Yahoo 知恵袋




中学数学 連立方程式 の効果的な教え方 小数 分数問題




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




分数の方程式の問題 解き方のコツは両辺に数をかけて分母を消せ 中学や高校の数学の計算問題




分母にxのある方程式の解き方を教えて頂けますか Okwave




いろいろな連立方程式 中学生 数学のノート Clear
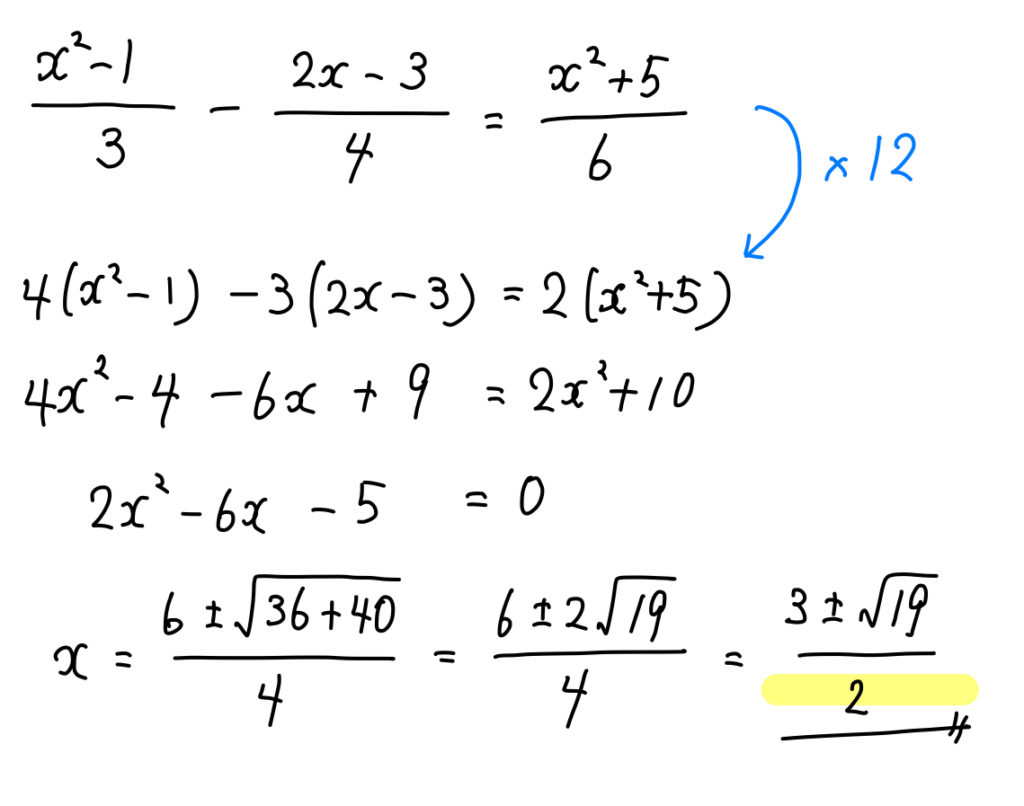



分数 小数 ルートを含む二次方程式の解き方まとめ 数スタ




画像の 3 のような分数と小数の混ざった連立方程式がわかりません 解 数学 教えて Goo
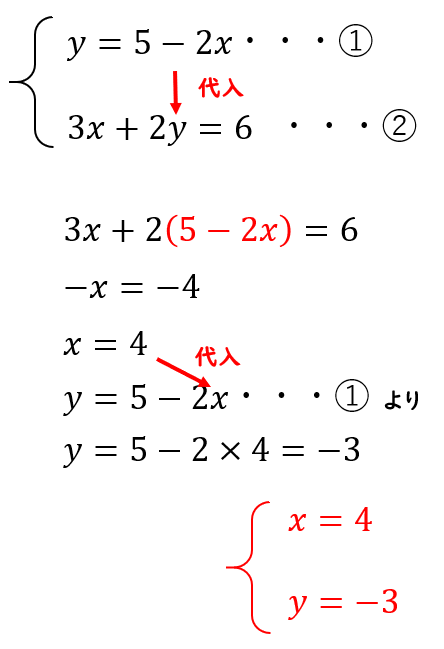



連立方程式の2つの解き方 代入法 加減法 数学fun




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット
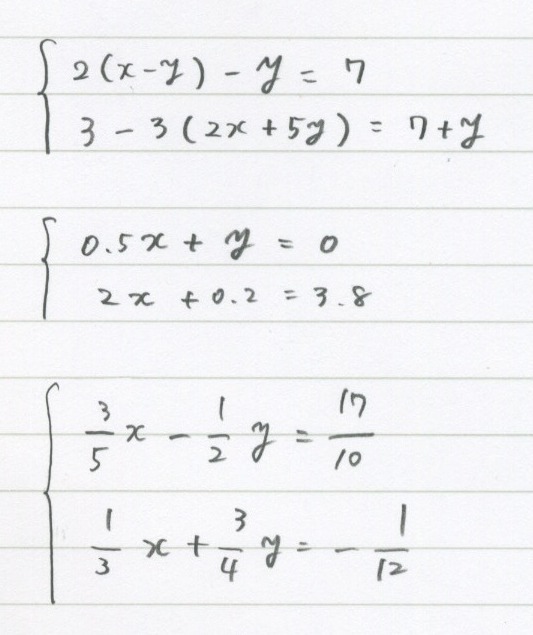



5 2 連立方程式 かっこや分数小数はもうできる 勉強できようサイト




小数の連立方程式の解き方 両辺を10倍や100倍しよう 中学や高校の数学の計算問題




この問題の解答に 両辺に12をかけるとあるのですが 右辺に12がかけられていないよう Clear




中学2年生 連立方程式 これテストに出ます ふるやまんのマスラボ奮闘記




数学 時短演習cote




連立方程式 割合の問題 おっかぁ Note




中2数学 カッコ 分数を含む連立方程式 例題編 映像授業のtry It トライイット




高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者




高校数学で学習する連立方程式の解き方まとめ 数スタ




中学2年数学 分数と小数の連立方程式 勉強 Youtube スタディチューブ




置き換えによる連立方程式 まなびの学園




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




高校数学 様々な2次方程式の解法 分数 小数 根号 置換 絶対値 受験の月




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス




置き換えによる連立方程式 まなびの学園
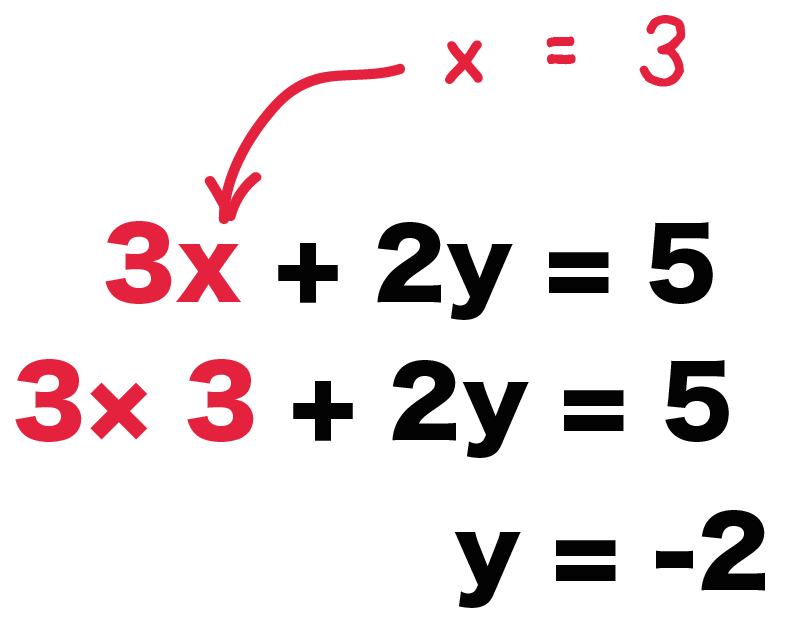



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく



連立方程式とは チーム エン




方程式の問題で分数のときは分母を通分すべきなのか 中学や高校の数学の計算問題




中2数学 カッコ 分数を含む連立方程式 練習編 映像授業のtry It トライイット




中学2年数学 分数と小数の連立方程式 Youtube




連立方程式 分数と整数が混じった計算の解き方をイチから解説 中学数学 理科の学習まとめサイト
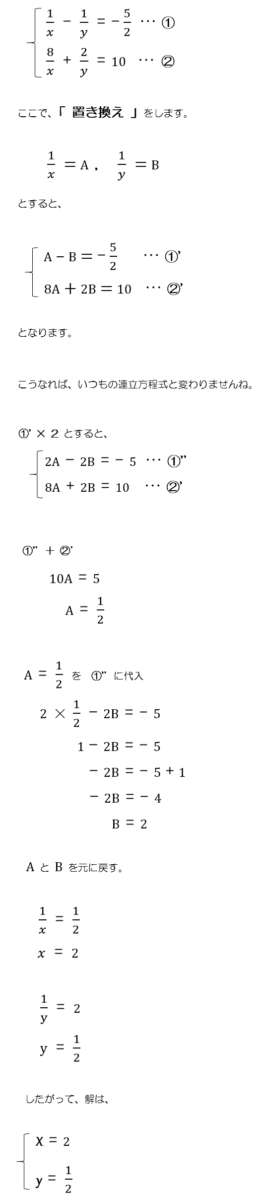



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬




連立方程式の解き方 係数に分数がふくまれる場合 Youtube
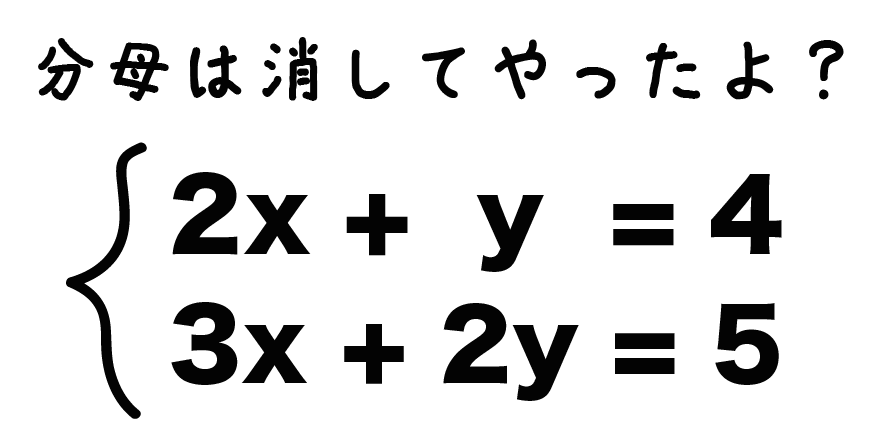



3分でわかる 分数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




中2数学 連立方程式 いろいろな連立方程式 4つのパターン たけのこ塾 勉強が苦手な中学生のやる気をのばす



1




分数をふくむ連立方程式 Youtube




連立方程式の代入法 簡単な問題で やり方をわかりやすく紹介 中学や高校の数学の計算問題



連立方程式の小数と分数の混ざった式について この問題が解 Yahoo 知恵袋




中学数学 連立方程式 小数 分数 中学数学の無料オンライン学習サイトchu Su



中学の数学 分数の連立方程式の解き方について質問です の両辺に15 Yahoo 知恵袋




連立方程式 分数ありバージョン 苦手な数学を簡単に



Q Tbn And9gcrfs1uvdsvk6gzavkllt3wnr9rtqv5hqsspffwnzsz9gceyd9 Usqp Cau




分数と小数の連立方程式の解き方が分かりません 教えてください Clear



中学数学 連立方程式 小数 分数 中学数学の無料オンライン学習サイトchu Su




中学1年生 数学 無料問題集 分数の一次方程式 おかわりドリル




この連立方程式の解き方を教えてください この連立方程式の解き方を教 数学 教えて Goo




中学数学 連立方程式 の効果的な教え方 小数 分数問題



連立方程式の解き方




分数と小数の連立方程式の解き方が分かりません 教えてください Clear



連立 方程式 計算 分数



連立方程式とグラフ
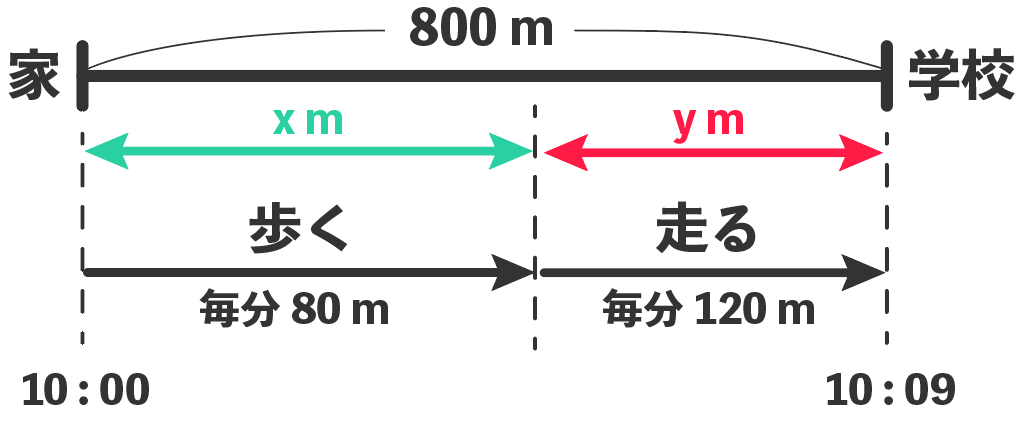



連立方程式の利用 速さ 道のり 時間の文章問題の解き方 Qikeru 学びを楽しくわかりやすく
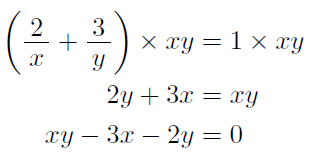



置き換えによる連立方程式 まなびの学園



中1 一次方程式の分数は整数になおそう 中学数学の方程式 中間 期末テスト 高校入試対策



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料




3分でわかる 小数をふくむ連立方程式の解き方 Qikeru 学びを楽しくわかりやすく




分数の連立方程式の解き方が分からないので教えてください お願いします Clear
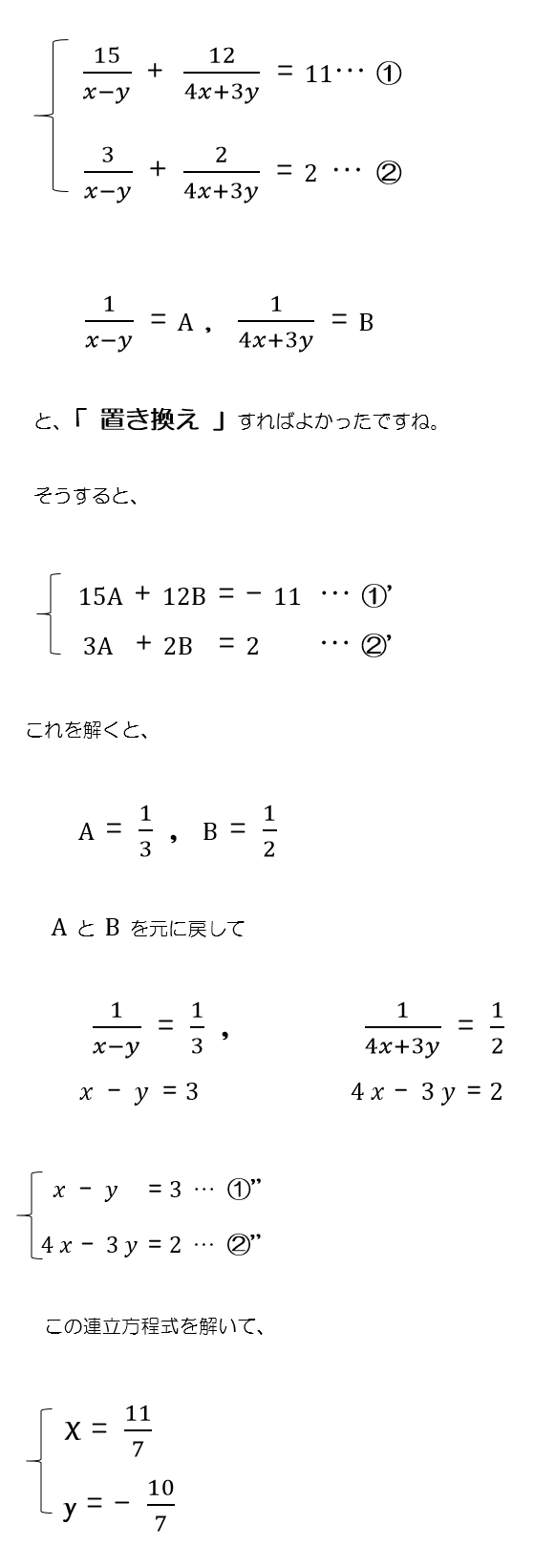



なるほど数学コラム 中学編 8 分母に文字がある連立方程式 を解こう Katekyo学院 教室で個別指導塾ならkatekyo学院 自宅でプロ家庭教師は福島県家庭教師協会 県内各地域で受講可能 福島 郡山 白河 会津 喜多方 いわき 相馬




連立方程式 いろいろな計算 無料で使える中学学習プリント




いろいろな連立方程式 かっこを含む 分数 小数を含む A B C 教遊者


